2 opties
Een computer kan niet werken zonder elektriciteit. En met elektriciteit heb je maar 2 opties: deze staat aan of uit. Er gaat wel of geen stroom door een elektriciteitsdraad. Deze 2 opties kun je ook representeren als een ja of nee, waar of niet waar, en in computers zie je dit terug als 1 en 0. De 1 betekent dat de elektriciteit aan staat en de 0 dat de elektriciteit uit staat. Zo’n 1 of 0 noemen we ook wel een ‘bit’. 1 Elektriciteitsdraad bestaat dus uit 2 bits. Hoe meer elektriciteitsdraden je gebruikt, hoe meer bits er dus zijn. En hoe meer bits je kunt gebruiken, hoe complexer data en informatie kunnen worden.
Het binaire systeem
Met deze bits kunnen we een binair systeem gebruiken. Binair betekent namelijk dat er maar 2 opties zijn. Om het uit te leggen, zullen we het vergelijken met het systeem dat we gebruiken wanneer wij als mensen tellen: het decimale systeem.
Decimaal
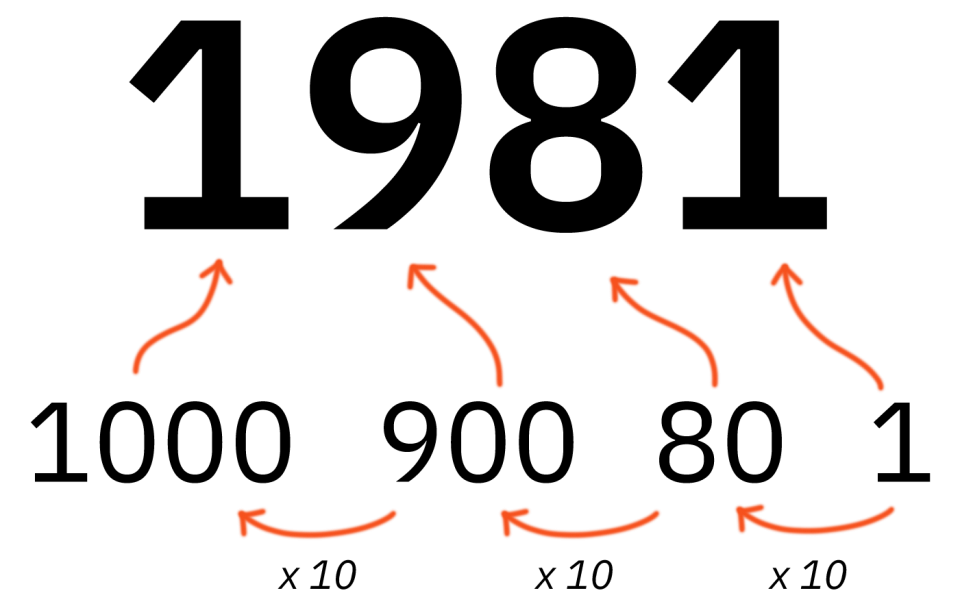
Het decimale systeem bestaat uit 10 cijfers. 0 tot 9. Kijk eens naar het nummer 1981, we hebben vroeger geleerd dat elke positie in zo’n nummer een waarde heeft. De eerste 1 in dit geval is een 1000ste, de 9 een 100e, in dit geval dus 900, de 8 een 10e, hier dus 80, en de 1 gewoon een 1. Met elke stap die je naar links gaat, vermenigvuldig je het getal met 10. De reeks gaat dus als volgt: 1 – 10 – 100 – 1000 – 10000 enzovoort.
Binair
Het binaire systeem bestaat maar uit 2 cijfers. 1 en 0. En in plaats van dat we met 10 vermenigvuldigen wanneer we een stap naar links gaan, vermenigvuldigen we met 2. De reeks gaat dus als volgt: 1 – 2 – 4 – 8 – 16 enzovoort.
Kijk eens naar het nummer 11001 hieronder. Het eerste cijfer helemaal rechts representeert een 1, de tweede een 2 en de derde een 4, maar omdat op de plek van de 2 en de 4 een 0 staat in plaats van een 1, tel die die niet mee. Daarna hebben we weer twee keer een 1, dit zijn 8 en 16. Alle plekken in de reeks waar een 1 staat tel je bij elkaar op, en zo kom je uit op een getal. In dit geval tel je dus 1 + 8 + 16 wat uitkomt op 25.

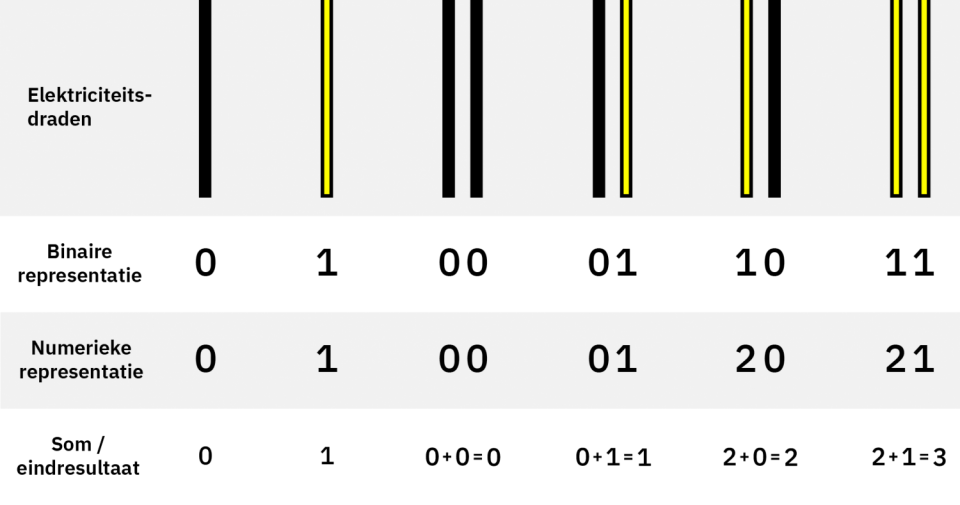
Met 1 elektriciteitsdraad zijn er maar 2 getallen beschikbaar, namelijk 0 en 1. Met 2 draden heb je 4 getallen tot je beschikking, namelijk 00, 01, 10, 11. Staan beide elektriciteitsdraden uit, dan is de binaire code 00, wat 0 representeert. Doe je de eerste aan en de tweede uit, dan is de binaire code 01, wat 1 representeert. Doe je de tweede aan en de eerste uit, dan is de binaire code 10, wat 2 representeert. Doe je allebei de elektriciteitsdraden aan, dan is de binaire code 11, wat 3 representeert, want 1 + 2 = 3.
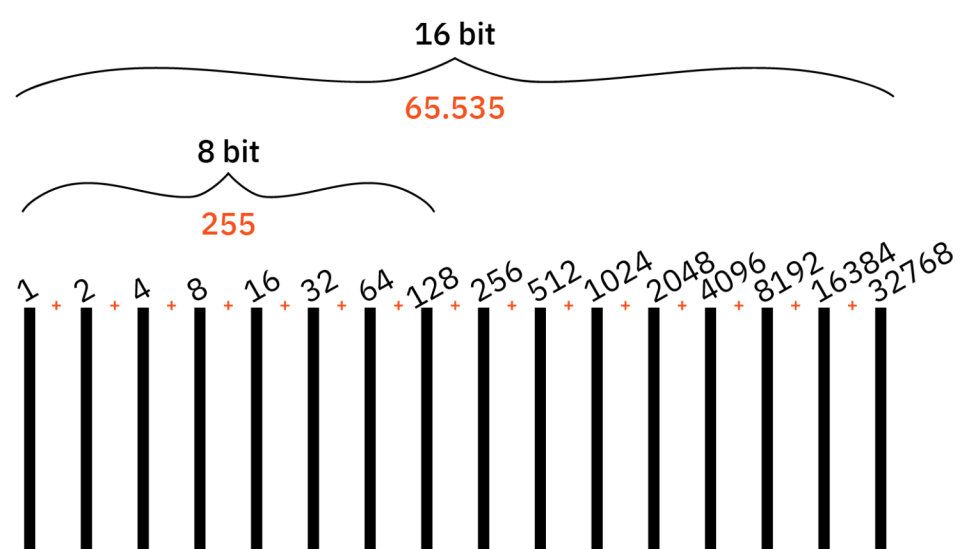
Hoe meer elektriciteitsdraden je dus gebruikt, hoe groter de getallen kunnen worden. Met 8 elektriciteitsdraden bijvoorbeeld, oftewel 8 bit, is de reeks 1 – 2 – 4 – 8 – 16 – 32 – 64 – 128. Als alle elektriciteitsdraden aan staan en je al deze nummers bij elkaar optelt, is het grootste nummer dat je kunt laten zien het nummer 255. Met 16 bit (en dus 16 elektriciteitsdraden) is het grootste nummer 65.535. Moet je nagaan wat je dan met 64 of zelfs 128 bit kan doen!
Tekst, afbeeldingen en muziek
De computers en apparaten die we vandaag de dag zien, gebruiken we niet alleen om getallen te berekenen. We gebruiken ze ook om dingen te kunnen zien, zoals tekst, afbeeldingen en muziek. Je leest deze blog toch ook op een computer of mobiel? Maar hoe zit dit dan in elkaar?
Dit soort informatie kunnen we ook verwerken in de vorm van die eentjes en nulletjes.
Tekst
Elke letter in het alfabet kun je een getal toewijzen. Welk getal elke letter heeft toegewezen gekregen is voor elke computer hetzelfde. Dit is namelijk vastgelegd in een standaard waar elke computer zich aan houdt. De 2 meest bekende standaarden zijn ASCII en Unicode. De hoofdletter A heeft bijvoorbeeld het getal 65 toegewezen gekregen, wat je in binaire code als 01000001 schrijft. De kleine letter a kreeg het getal 97, wat in binaire code 01100001 is.

Afbeeldingen
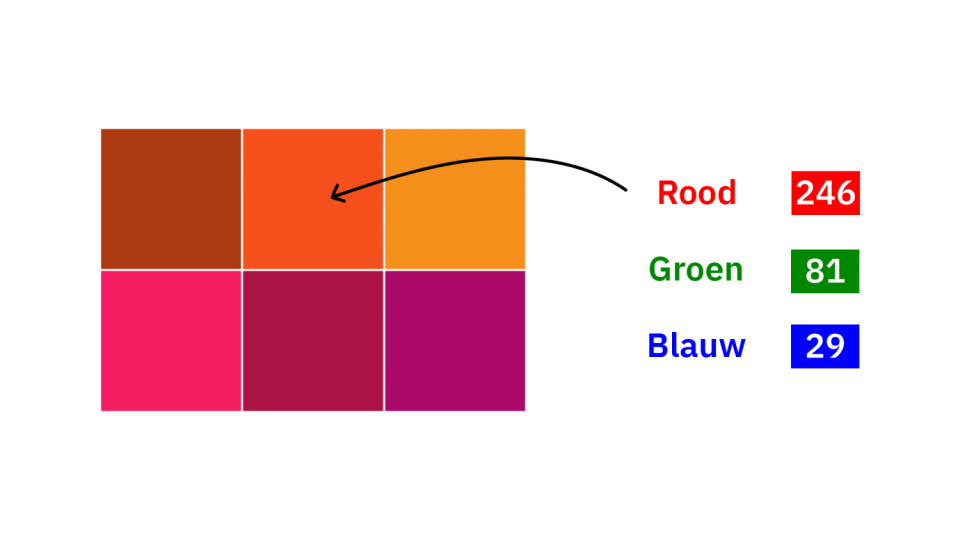
Elke afbeelding, video en andere grafische representatie bestaat uit pixels. Een pixel bevat een kleur. In dit geval is het een combinatie van rood, groen en blauw, oftewel RGB. Elk van deze kleur heeft 255 mogelijkheden. Dus 255 tinten rood, 255 tinten groen en 255 tinten blauw. Hiermee kun je in totaal maar liefst 16.777.216 kleurcombinaties maken! En die kleuren kun je ook weer in binaire code omzetten voor een computer om te lezen.
Wat betreft video werkt het vrijwel hetzelfde. Een video is namelijk een reeks afbeeldingen achter elkaar. Wanneer een video opgenomen is in 25fps, oftewel 25 frames per second, wil dat zeggen dat elke seconde video 25 afbeeldingen is. Een video bevat dus ontzettend veel binaire informatie.
Muziek
Geluid bestaat uit vibraties in de lucht. Die vibraties kunnen we in een golfvorm laten zien. En elk punt in de golfvorm kun je weer een getal geven. En elk getal kun je weer omzetten naar binaire code. En hoe meer bits je hebt, hoe meer punten in de golfvorm je kunt opslaan en hoe beter je geluidskwaliteit dus is.
Dit is ook waarom afbeeldingen, video’s en muziek een bepaalde bestandsgrootte hebben. Zeggen de afkortingen kB, MB en GB je misschien wat? Dit zijn dus al die bits die al onze data opslaan.
8 bits bij elkaar noemen we 1 byte. Dit is genoeg voor het opslaan van 1 letter of symbool.
1000 bytes noemen we een kilobyte, of 1kB.
1000kB is 1 megabyte of MB.
1000MB is 1 gigabyte of GB.
1000GB is 1 terabyte of TB.
En ga zo maar door!
Je hebt bijvoorbeeld gemiddeld 30MB aan opslag nodig om alle binaire code op te slaan die een liedje vormen. Dezelfde principes gelden voor afbeeldingen en video’s.
Binaire code staat aan de basis van elke computer. En een computer kun je voor van alles gebruiken. Zoals bijvoorbeeld voor het lezen van deze blog! Hiervoor heb je natuurlijk internet nodig, maar hoe werkt dat nu eigenlijk? Dat zal in de volgende blog aangepakt worden.


